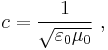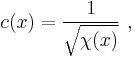Fock–Lorentz symmetry

Lorentz invariance follows from two independent postulates: the principle of relativity and the principle of constancy of the speed of light. Dropping the latter while keeping the former leads to a new invariance, known as Fock–Lorentz symmetry[1] or the Projective Lorentz Transformation.[2][3] The general study of such theories began with Fock,[4] who was motivated by the search for the general symmetry group preserving relativity without assuming the constancy of c.

This invariance does not distinguish between inertial frames (and therefore satisfies the principle of relativity) but it allows for a varying speed of light in space c; indeed it allows for a non-invariant c. According to Maxwell's equations the speed of light satisfies

c = \frac{1}{\sqrt{\varepsilon _0 \mu_0} }\ ,

with ε0, μ0 the electric constant and magnetic constant. If the speed of light depends upon the space-time coordinates of the medium, say x, then:

c(x) = \frac{1}{\sqrt{\chi (x) } }\ ,

where χ(x) represents the vacuum as a variable medium.[5]

See also

References

  1. ^ João Magueijo (2000). "Covariant and locally Lorentz-invariant varying speed of light theories". Phys Rev D62 (10). arXiv:gr-qc/0007036. Bibcode 2000PhRvD..62j3521M. doi:10.1103/PhysRevD.62.103521. 
  2. ^ S.N.Manida (1999). "Fock-Lorentz transformations and time-varying speed of light". ArXiv preprint: 5046. arXiv:gr-qc/9905046. Bibcode 1999gr.qc.....5046M. 
  3. ^ Sergey S. Stepanov (1999). "A time-space varying speed of light and the Hubble Law in static Universe". Phys Rev D62 (2). arXiv:astro-ph/9909311. Bibcode 2000PhRvD..62b3507S. doi:10.1103/PhysRevD.62.023507. 
  4. ^ Vladimir Aleksandrovich Fock (1964). The theory of space, time and gravitation (2 ed.). Macmillan. ISBN 0080100619. http://books.google.com/?id=dSEvAAAAIAAJ&dq=intitle:The+intitle:Theory+intitle:of+intitle:Space+intitle:Time+intitle:and+intitle:Gravitation. 
  5. ^ J. W. Moffat (2001). "A Model of Varying Fine Structure Constant and Varying Speed of Light". ArXiv preprint: 9350. arXiv:astro-ph/0109350. Bibcode 2001astro.ph..9350M. 

Further reading